From Oleg D. Jefimenko, Causality, Electromagnetic Induction, and Gravitation: A Different Approach to the Theory of Electromagnetic and Gravitational Fields, 2nd ed., (Electret Scientific, Star City, 2000) This reproduction of Heaviside's article is an unedited copy of the original, except that I have converted some formulas and all vector equations appearing in the article to modern mathematical notation.
A GRAVITATIONAL AND ELECTROMAGNETIC ANALOGY. BY OLIVER HEAVISIDE. [Part I, The Electrician, 31, 281-282 (1893)] To form any notion at all of the flux of gravitational energy, we must first localise the energy. In this respect it resembles the legendary hare in the cookery book. Whether the notion will turn out to be a useful one is a matter for subsequent discovery. For this, also, there is a well-known gastronomical analogy.
Now, bearing in mind the successful manner in which Maxwell's localisation of electric and magnetic energy in his ether lends itself to theoretical reasoning, the suggestion is very natural that we should attempt to localise gravitational energy in a similar manner, its density to depend upon the square of the intensity of the force, especially because the law of the inverse squares is involved throughout.
Certain portions of space are supposed to be occupied by matter, and its amount is supposed to be invariable. Furthermore, it is assumed to have personal identity, so that the position and motion of a definite particle of matter are definite, at any rate relative to an assumed fixed space. Matter is recognised by the property of inertia, whereby it tends to persist in the state of motion it possesses; and any change in the motion is ascribed to the action of force, of which the proper measure is, therefore, the rate of change of quantity of motion, or momentum.
Letbe the density of matter, and e the intensity of force, or the force per unit matter, then
expresses the moving force on (1)
, which has its equivalent in increase of the momentum. There are so many forces nowadays of a generalised nature, that perhaps the expression "moving force" may be permitted for distinctness, although it may have been formerly abused and afterwards tabooed.
Now the force F, or the intensity e, may have many origins, but the only one we are concerned with here is the gravitational force. This appears to depend solely upon the distribution of the matter, independently of other circumstances, and its operation is concisely expressed by Newton's law, that there is a mutual attraction between any two particles of matter, which varies as the product of their masses and inversely as the square of their distance. Let e now be the intensity of gravitational force, and F the resultant moving force, due to all the matter. Then e is the space-variation of a potential, say,and the potential is found from the distribution of matter by (2)
where c is a constant. This implies that the speed of propagation of the gravitative influence is infinitely great. (3)
Now when matter is allowed to fall together from any configuration to a closer one, the work done by the gravitational forcive is expressed by the increase made in the quantity. This is identically the same as the quantity
summed through all space. If, for example, the matter be given initially in a state of infinitely fine division, infinitely widely separated, then the work done by the gravitational forcive in passing to any other configuration is
or
, which therefore expresses the "exhaustion of potential energy." We may therefore assume that ce2/2 expresses the exhaustion of potential energy per unit volume of the medium. The equivalent of the exhaustion of potential energy is, of course, the gain of kinetic energy, if no other forces have been in action.
We can now express the flux of energy. We may compare the present problem with that of the motion of electrification. If moved about slowly in a dielectric, the electric force is appreciably the static distribution. Nevertheless, the flux of energy depends upon the magnetic force as well. It may, indeed, be represented in another way, without introducing the magnetic force, but then the formula would not be sufficiently comprehensive to suit other cases. Now what is there analogous to magnetic force in the gravitational case? And if it have its analogue, what is there to correspond with electric current? At first glance it might seem that the whole of the magnetic side of electromagnetism was absent in the gravitational analogy. But this is not true.
Thus, if u is the velocity of, then
is the density of a current (or flux) of matter. It is analogous to a convective current of electrification. Also, when the matter
enters any region through its boundary, there is a simultaneous convergence of gravitational force into that region proportional to
. This is expressed by saying that if
then C is a circuital flux. It is the analogue of Maxwell's true current; for although Maxwell did not include the convective term (4)
, yet it would be against his principles to ignore it. Being a circuital flux, it is the curl of a vector, say
This defines h except as regards its divergence, which is arbitrary, and may be made zero. Then h is the analogue of magnetic force, for it bears the same relation to flux of matter as magnetic force does to convective current. We have (5)
if A = Pot C. But, since instantaneous action is here involved, we may equally well take (6)
and its curl will be h. Thus, whilst the ordinary potential P is the potential of the matter, the new potential A is that of its flux. (7)
Now if we multiply (5) by e, we obtainor, which is the same, (8)
if U = ce2/2. But (9)
represents the rate of exhaustion of potential energy, so -
represents its rate of increase, whilst
represents the activity of the force on
, increasing its kinetic energy. Consequently, the vector
expresses the flux of' gravitational energy. More strictly, any circuital flux whatever may be added. This
is analogous to the electromagnetic
found by Poynting and myself. But there is a reversal of direction. Thus, comparing a single moving particle of matter with a similarly-moving electric charge, describe a sphere round each. Let the direction of motion be the axis, the positive pole being at the forward end. Then in the electrical case the magnetic force follows the lines of latitude with positive rotation about the axis, and the flux of energy coincides with the lines of longitude from the negative pole to the positive. But in the gravitational case, although h still follows the lines of latitude positively, yet since the radial e is directed to instead of from the centre, the flux of energy is along the lines of longitude from the positive pole to the negative. This reversal arises from all matter being alike and attractive, whereas like electrifications repel one another.
The electromagnetic analogy may be pushed further. It is as incredible now as it was in Newton's time that gravitative influence can be exerted without a medium; and, granting a medium, we may as well consider that it propagates in time, although immensely fast. Suppose, then, instead of instantaneous action, which involveswe assert that the gravitational force e in ether is propagated at a single finite speed v. This requires that (10)
for this is the general characteristic of undissipated propagation at finite speed. Now, (11)
so in space free from matter we have 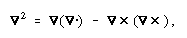
But we also have, by (5), (12)
away from matter. This gives a second value to (13)
, when we differentiate (13) to the time, say
So, by (12) and (14), and remembering that we have already chosen h circuital, we derive (14)
Or, if (15)
is a new constant, such that
then (15) may be written in the form (16)
To sum up, the first circuital law (5), or (17)
leads to a second one, namely (17), if we introduce the hypothesis of propagation at finite speed. (18)
This, of course, might be inferred from the electromagnetic case.
In order that the speed v should be not less than any value that may be settled upon as the least possible, we have merely to makebe of the necessary smallness. The equation of activity becomes, instead of (9),
if (3)
. The negative sign before the time-increase of this quantity points to exhaustion of energy, as before. If so, we should still represent the flux of energy by
. But, of course, T is an almost vanishing quantity when is small enough, or v big enough. Note that h is not a negligible quantity, though the product
is. Thus results will be sensibly as in the common theory of instantaneous action, although expressed in terms of wave-propagation. Results showing signs of wave-propagation would require an inordinately large velocity of matter through the ether. It may be worth while to point out that the lines of gravitational force connected with a particle of matter will no longer converge to it uniformly from all directions when the velocity v is finite, but will show a tendency to lateral concentration, though only to a sensible extent when the velocity of the matter is not an insensible fraction of v.
The gravitational-electromagnetic analogy may be further extended if we allow that the ether which supports and propagates the gravitational influence can have a translational motion of its own, thus carrying about and distorting the lines of force. Making allowance for this convection of e by the medium, with the concomitant convection of h, requires us to turn the circuital laws (17), (18) to(19)
where q is the velocity of the medium itself. (20)
It is needless to go into detail, because the matter may be regarded as a special and simplified case of my investigation of the forces in the electromagnetic field, with changed meanings of the symbols. It is sufficient to point out that the stress in the field now becomes prominent as a working agent. It is of two sorts, one depending upon e and the other upon h, analogous to the electric and magnetic stresses. The one depending upon h is, of course, insignificant. The other consists of a pressure parallel to e combined with a lateral tension all round it, both of magnitude ce2/2. This was equivalently suggested by Maxwell. Thus two bodies which appear to attract are pushed together. The case of two large parallel material planes exhibits this in a marked manner, for e is very small between them, and relatively large on their further sides.
But the above analogy, though interesting in its way, and serving to emphasise the non-necessity of the assumption of instantaneous or direct action of matter upon matter, does not enlighten us in the least about the ultimate nature of gravitational energy. It serves, in fact, to further illustrate the mystery. For it must be confessed that the exhaustion of potential energy from a universal medium is a very unintelligible and mysterious matter. When matter is infinitely widely separated, and the forces are least, the potential energy is at its greatest, and when the potential energy is most exhausted, the forces are most energetic!
Now there is a magnetic problem in which we have a kind of similarity of behaviour, viz., when currents in material circuits are allowed to attract one another. Let, for completeness, the initial state be one of infinitely wide separation of infinitely small filamentary currents in closed circuits. Then, on concentration to any other state, the work done by the attractive forces is represented by, where is the inductivity and H the magnetic force. This has its equivalent in the energy of motion of the circuits, or may be imagined to be so converted, or else wasted by friction, if we like. But, over and above this energy, the same amount,
, represents the energy of the magnetic field, which can be got out of it in work. It was zero at the beginning. Now, as Lord Kelvin showed, this double work is accounted for by extra work in the batteries or other sources required to maintain the currents constant. (I have omitted reference to the waste of energy due to electrical resistance, to avoid complications.) In the gravitational case there is a partial analogy, but the matter is all along assumed to be incapable of variation, and not to require any supply of energy to keep it constant. If we asserted that ce2/2 was stored energy, then its double would be the work done per unit volume by letting bodies attract from infinity, without any apparent source. But it is merely the exhaustion of potential energy of unknown amount and distribution.
Potential energy, when regarded merely as expressive of the work that can be done by forces depending upon configuration, does not admit of much argument. It is little more than a mathematical idea, for there is scarcely any physics in it. It explains nothing. But in the consideration of physics in general, it is scarcely possible to avoid the idea that potential energy should be capable of localisation equally as well as kinetic. That the potential energy may be itself ultimately kinetic is a separate question. Perhaps the best definition of the former is contained in these words :--Potential energy is energy that is not known to be kinetic. But, however this be, there is a practical distinction between them which it is found useful to carry out. Now, when energy can be distinctly localised, its flux can also be traced (subject to circuital indeterminateness, however). Also, this flux of energy forms a useful working idea when action at a distance is denied (even though the speed of transmission be infinitely great, or be assumed to be so). Any distinct and practical localisation of energy is therefore a useful step, wholly apart from the debatable question of the identity of energy advocated by Prof. Lodge.
From this point of view, then, we ought to localise gravitational energy as a preliminary to a better understanding of that mysterious agency. It cannot be said that the theory of the potential energy of gravitation exhausts the subject. The flux of gravitational energy in the form above given is, perhaps, somewhat more distinct, since it considers the flux only and the changes in the amount localised, without any statement of the gross amount. Perhaps the above analogy may be useful, and suggest something better.
[Part II, The Electrician, 31, 359 (1893)] In my first article on this subject (The Electrician, July 14, 1893, p.281), I partly assumed a knowledge on the part of the reader of my theory of convective currents of electrification ("Electrical Papers," Vol. II., p. 495 and after), and only very briefly mentioned the modified law of the inverse squares which is involved, viz., with a lateral concentration of the lines of force. The remarks of the Editor(1) and of Prof. Lodge(2) on gravitational aberration, lead me to point out now some of the consequences of the modified law which arises when we assume that the ether is the working agent in gravitational effects, and that it propagates disturbances at speed v in the manner supposed in my former article. There is, so far as I can see at present, no aberrational effect, but only a slight alteration in the intensity of force in different directions round a moving body considered as an attractor.
Thus, take the case of a big Sun and small Earth, of masses S and E, at distance r apart. Let f be the unmodified force of S on E, thususing rational units in order to harmonise with the electromagnetic laws when rationally expressed. Also, let F be the modified force when the Sun is in motion at speed u through the ether. Then(3) (1)
where s is the small quantity u2/v2, and (2)
is the angle between r and the line of motion. ("Electrical Papers," Vol. II., pp. 495, 499).
Therefore, if the Sun is at rest, there is no disturbance of the Newtonian law, because its " field of force" is stationary. But if it has a motion through space, there is a slight weakening of the force in the line of motion, and a slight strengthening equatorially. The direction is still radial.
To show the size of the effect, letu = 3 107 centim. per sec. v = 3 1010 centim. per sec. (3) This value of u is not very different from the speed attributed to fast stars, and the value of v is the speed of light itself.
So we havei.e., one millionth. All perturbing forces of the first order are, therefore, of the order of magnitude of only one-millionth of the full force, even when the speed of propagation is as small as that of light. (4)
The simplest case is when the common motion of the Sun and Earth is perpendicular to the plane of the orbit. Then, all round the orbit, and
showing increase in the force of attraction of S on E of one two-millionth part, without alteration of direction or variation in the orbit.(4) (5)
But when the common motion of the Sun and Earth is in their plane,varies from 0 to
in a revolution, so that the attraction on E, whilst towards the Sun's centre, always undergoes a periodic variation from
when (6)
= 0, to
when (7)
. The extreme variation is, therefore, 3sf/2, according to the data used. The result is a slight change in the shape of the orbit.
But, to be consistent, having made v finite by certain suppositions, we should carry out the consequences more fully, and allow not merely for the change in the Newtonian law, as above, but for the force brought in by the finiteness of v which is analogous to the "electromagnetic force." This is very small truly, but so is the above change in the Newtonian law, and since they are of the same order of magnitude, we should also count the auxiliary force. Call it G. Thenwhere F is as before, in (2) above, q is the actual speed of the Earth (not the same as u), and in the third vectorial factor q1, u1, and r1 are unit vectors drawn parallel to the direction of the Earth's motion, of the Sun's motion, and from the Sun to the Earth. We see at once that the order of magnitude cannot be greater than that of the departure of F from f before considered, because u and q will be of the same order, at least when u is big. As for x, it is simply a numerical factor, which cannot exceed 1, and is probably 2/3 (8)
The simplest case is when the motion of the Sun is perpendicular to the orbit of the Earth. Thengives the tensor(5) or size of the auxiliary force. It is radial, but outwards, so that the result is merely to reduce the size of' the previous correction, viz., the difference of F from f in the same motional circumstances.
(9)
But when the line of motion of Sun is in the plane of the orbit, the case is much more complicated. The force G is neither constant (for the same distance) nor radial, except in four positions, viz., two in the line of motion of the Sun, when the auxiliary force vanishes, and two when, when it is greatest. But this force is still in the plane of the orbit, which is an important thing, and is, moreover, periodic, so that the tangential component is as much one way as the other in a period.
All we need expect, then, so far as I can see from the above considerations, are small perturbations due to the variation of the force of gravity in different directions, and to the auxiliary force. Of course, there will be numerous minor perturbations
If variations of the force of the size considered above are too small to lead to observable perturbations of motion, then the striking conclusion is that the speed of gravity may even be the same as that of light. If they are observable, then, if existent, they should turn up, but if non-existent then the speed of gravity should be greater. Furthermore, it is to be observed that there may be other ways of expressing the propagation of gravity.
But I am mindful of the good old adage about the shoemaker and his last, and am, therefore, reluctant to make any more remarks about perturbations. The question of the ether in its gravitational aspect must be faced, however, and solved sooner or later, if it be possible. Perhaps, therefore, my suggestions may not be wholly useless.
1. The Electrician, July 14, p. 277, and July 23, p. 340.2. The Electrician, July 28, p. 347.
3. This is the case of steady motion. There is no simple formula when the motion is unsteady.
4. But Prof. Lodge tells me that our own particular Sun is considered to move only 109 miles per second. This is stupendously slow. The size of s is reduced to about 1/360 part of that in the text, and the same applies to the corrections depending upon it.
5. Heaviside uses the word "tensor" for the magnitude of a force vector (O. D. J.).
